Linked list considered useless
I have found this talk by Bjarne Stroustrup about inefficiency of linked lists. The arguments he presents are:
- Linked lists has asymptotic insertion time of $O(1)$, however dynamic arrays $O(n)$. He assumes that you rarely insert into a priori known location and thus you first need to perform $O(n)$ search in the linked list. Asymptotically linked lists are thus equivalent to dynamic arrays and in reality they are inferior because of higher memory indirection.
- Linked lists are less memory-efficient as they have to store a pair of pointers with each item.
Is it measurable?
Yes, it is. I wrote a simple program to compare the behavior of insertion to
the std::vector<int> and std::list<int>.
/*
* Compile with:
* g++ -std=c++11 -O3 -o linked_list linked_list.cpp
*/
#include <algorithm>
#include <chrono>
#include <iostream>
#include <list>
#include <random>
#include <string>
#include <vector>
using namespace std::chrono;
template <typename T>
void generate(T &container, const size_t n, const int seed = 0) {
for (int i = 0; i < n; ++i) {
container.push_back(i);
}
}
template <typename T>
void copy(const T &src_container, T &dst_container) {
dst_container = T(src_container);
/* To emulate copy usage */
std::cerr << dst_container.size() << std::endl;
}
template <typename T>
void insertions(T &container, const size_t n, const size_t max_val,
const int seed = 1) {
std::mt19937 generator(seed);
std::uniform_int_distribution<int> distribution(0, max_val);
/* Generate random value and insert it to proper (sorted) position */
for (int i = 0; i < n; ++i) {
auto value = distribution(generator);
auto it = std::find_if(container.begin(), container.end(),
[value](const int v) {
return v > value;
});
container.insert(it, value);
}
}
template <typename T>
inline long long format_duration(const T begin, const T end) {
return duration_cast<nanoseconds>(end - begin).count();
}
template <typename T>
void measure(const int size, const int test_size, const std::string &tag) {
typedef steady_clock clock_t;
T fixture;
time_point<clock_t> begin, end;
/* Generate */
begin = steady_clock::now();
generate(fixture, size);
end = steady_clock::now();
std::cout << "generate:" << tag << "\t" << size << "\t" <<
format_duration(begin, end) << "\t" << std::endl;
/* Copy */
T fixture2;
begin = steady_clock::now();
copy(fixture, fixture2);
end = steady_clock::now();
std::cout << "copy:" << tag << "\t" << size << "\t" <<
format_duration(begin, end) << "\t" << std::endl;
/* insertions */
begin = steady_clock::now();
insertions(fixture2, test_size, size);
end = steady_clock::now();
std::cout << "insertions:" << tag << "\t" << size << "\t" <<
format_duration(begin, end) << "\t" << std::endl;
}
int main(int argc, char *argv[]) {
for (int i = 0; i < 9; ++i) {
const int size = 1 << (i + 10);
measure<std::vector<int>>(size, size / 2, "vector");
measure<std::list<int>>(size, size / 2, "list");
}
return 0;
}The results of the mentioned program are bellow.
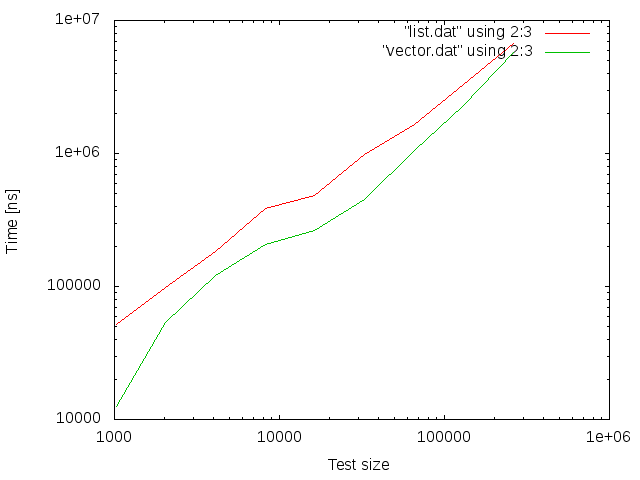
Appending to vector and to linked list seems to be comparable as the size of the container increases.
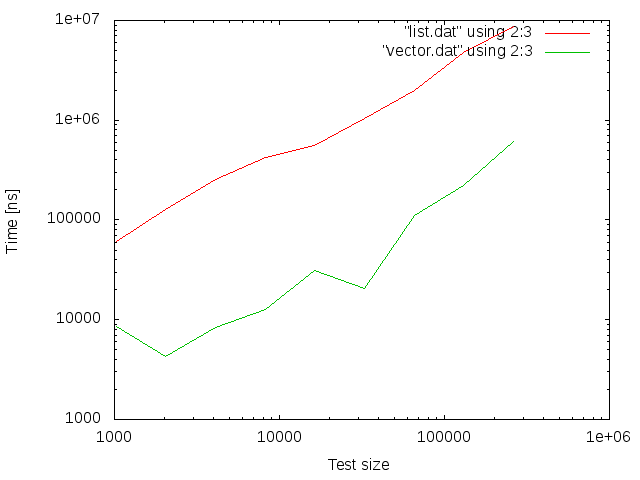
Copying the whole structures seems to be ~6 times faster for vector.
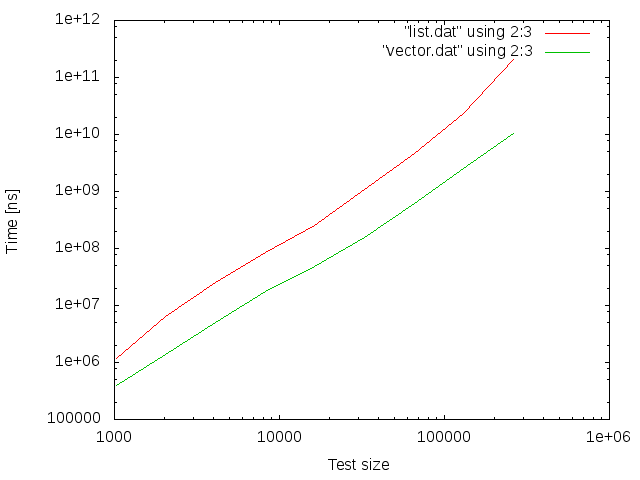
This is the case described by Stroustrup where vectors are faster even though inserted item has to shift all following items. Vector is consistently faster.
Moral of the story
Obviously, I’m not the only one who was influenced by this video. I was trying to list some arguments when/why linked lists are preferable.
Linked lists apologia
- Academic use when teaching students principles of dynamic data structures and pointers.
- Conservative memory footprint. This applies to the case when we are storing large structures where size of pointers is negligible to the size of the structures.
- Large structures where copying whole structure would be bothersome (as that’s what dynamic arrays had to do from time to time).
- Structures that are accessed directly via pointer (e.g. structures of OS kernel), list operations are then desired $O(1)$.
- Concurrent structures. Not sure about this but linked lists are more suitable for RCU.